简介
并查集是一种非常简单的数据结构,它主要涉及两个基本操作,分别为:
1. 合并两个不相交集合;
2. 判断两个元素是否属于同一个集合;
实现
实现上,通常用一个数组实现,如100个元素可以用大小为100的数组, 数组的内容存储节点的父亲节点的下标.
1.朴素实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
| public class UnionFind extends AbstractUnionFind {
/**
* ctor
* @param size
*/
public UnionFind(int size) {
assert(size > 0);
value = new int[size];
init();
}
/**
* 初始化数据
*/
private void init() {
assert (value != null && value.length > 0);
for (int i = 0; i < value.length; i++) {
value[i] = DEFAULT_PARENT; //DEFAULT_PARENT为-1
}
}
/**
* 合并根节点为rx 和 根节点为ry的树
* 这里rx 和 ry为下标
*
* @param rx
* @param ry
*/
@Override
public void Union(int rx, int ry) {
assert (rx >= 0 && rx < value.length);
assert (ry >= 0 && ry < value.length);
//找到两个节点的根节点
int px = Find(rx);
int py = Find(ry);
//将px设置为py的子树
value[px] = py;
}
/**
* 查找节点x的根节点
*
* @param x
* @return
*/
@Override
public int Find(int x) {
while(isRoot(x) == false) {
x = value[x];
}
return x;
}
/**
* 判断节点是否为根节点
*
* @param rx
* @return
*/
private boolean isRoot(int rx) {
assert (rx >= 0 && rx < value.length);
return value[rx] == DEFAULT_PARENT; //DEFAULT_PARENT为-1
}
}
|
Find的时间复杂度和树的高度成正比,最坏的情况下为所有节点形成一个链表, 这时候的复杂度为O(N);
Unoin时间需要调用Find,所以Union的最坏时间复杂度也为O(N);
2.优化1:根据树高度Union
朴素实现的容易出现所有节点(或者很多节点)形成一个链表,导致树的高度很大,进而导致Find的效率低.
我们可以简单的改变Union的策略,将小数(高度小)合并作为大树(高度大)的子树,高度也称之为树的秩.
实现这个策略,通常实现都是使用额外的一个数组来保存树的秩,在<数据结构与算法分析:C语言描述>这本书给出了一个巧妙的实现,我们value[rx]之前是用-1表示其为跟节点,这个-1完全是无意义的,我们可以用这个空间来保存树的高度,同时为了避免和下表混淆,我们保存高度的负值.
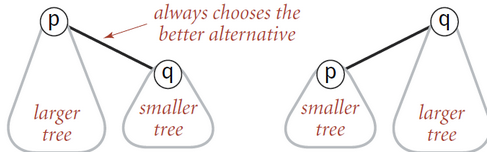
实现和朴实并查集的不同的地方:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
| /**
* 合并根节点为rx 和 根节点为ry的树
* 这里rx 和 ry为下标
*
* @param rx
* @param ry
*/
@Override
public void Union(int rx, int ry) {
assert (rx >= 0 && rx < value.length);
assert (ry >= 0 && ry < value.length);
//找到两个节点的根节点
int px = Find(rx);
int py = Find(ry);
// 将px设置为py的子树
if (value[px] < value[py]) { // px为根节点的树高度更大, 应该将py树作为px的子树
value[py] = px;
} else if (value[py] < value[px]) {
value[px] = py;
} else { // 高度相同, 最终树的高度+1
value[py] = px;
value[px]--; // 数的高度+1
}
}
/**
* 判断节点是否为根节点
*
* @param rx
* @return
*/
private boolean isRoot(int rx) {
assert (rx >= 0 && rx < value.length);
return value[rx] < 0; //小于0的都表示是跟节点
}
|
根据树高度Union基本能够使得树的高度维持在log(n)的级别,因此Find和Union的时间复杂度均为log(n);
3.优化2:路径压缩
路径压缩是指,我们在Find的过程中,从最底层节点依次遍历到根节点,期间我们可以将路径上的所以节点的父亲节点设置为根节点.
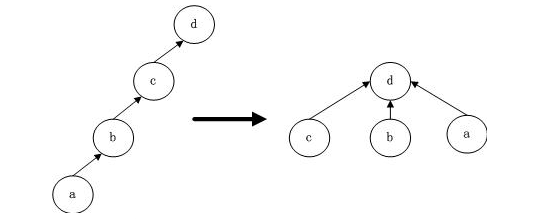
和2的不同之处:
```java
/*
* 查找节点x的根节点
* 从最底端往上便利的时候, 可以顺带更改每个节点的父亲节点为跟节点, 使得树的高度降低
*
* @param x
* @return
/
@Override
public int Find(int x) {
while(value[x] >= 0) { //非根节点
value[x] = Find(value[x]); //设置当前节点的父亲节点为根节点
}
return x;
}
不用担心递归的深度,因为从最开始就执行路径压缩的话,我们可以认为数的高度一直是1.
这是的树的高度基本为1,因此Unoin和Find的时间复杂度都接近O(1);
典型应用
并查集是高效简洁数据结构的典型代表.其典型应用包括:
无向图的连通分量个数
Kruskar算法求最小生成树

